RAPOSa

What's RAPOSa?

RAPOSa is a global optimization solver, specifically designed for mixed-integer polynomial programming problems with box-constrained variables. Written entirely in C++, it is based on the Reformulation-Linearization Technique developed by Hanif D. Sherali and Cihan H. Tuncbilek [1] and subsequently improved by Hanif D. Sherali, Evrim Dalkiran and collaborators [2] [3] [4].

Run directly on NEOS Server or from AMPL, Pyomo, JuMP or nl files

RAPOSa currently solves problems directly from AMPL, Pyomo, JuMP and via a .nl input file obtained with AMPL, Pyomo or JuMP. RAPOSa also solves problems directly from a .nl file. See the examples section for more information. One can also run RAPOSa on NEOS Server using this link.

You choose the auxiliary solvers

RAPOSa leans on two subsolvers, one for the auxiliary linear subproblems and one local optimizer. They are used to generate lower and upper bounds, respectively. To date, RAPOSa can connect with the following subsolvers (some free and some commercial).

• Supported (mixed-integer) linear solvers
  • Gurobi ⁽¹⁾ (commercial license, limited academic license also available)
  • Google OR-Tools (compatible with a variety of free and comercial solvers)
• Supported (mixed-integer) non-linear local solvers
  • Knitro ⁽²⁾ (commercial license)
  • Ipopt (free license)
  • Bonmin (free license)
  • CONOPT ⁽²⁾ (commercial license)
  • MINOS ⁽²⁾ (commercial license)

The best results are obtained with Gurobi and Knitro and the best results without a commercial subsolver are obtained with Glop (through Google OR-Tools) and Ipopt.

⁽¹⁾ If you want to use Gurobi, you must have a gurobi license.

⁽²⁾ If you want to use Knitro, CONOPT or MINOS, you must have the corresponding solver with its license.

Sequential or parallel version, you choose

The branch-and-bound scheme in which the Reformulation Linearization Technique is based takes great advantage of current parallelization procedures. A parallel version of RAPOSa is also available (on demand). It can benefit on the number of cores you have access to and which can improve significantly the performance of the algorithm.

Features

• Implementation of the basic RLT algorithm introduced in [1]
• Efficient generation of bound factors via J-Sets
• Warm start of LP solver at each node (just for Gurobi)
• Warm generation of J-Sets at each node
• Products of constraint factors and bound factors
• Bound tightening techniques
• SDP cuts
• Different branching criteria

Performance

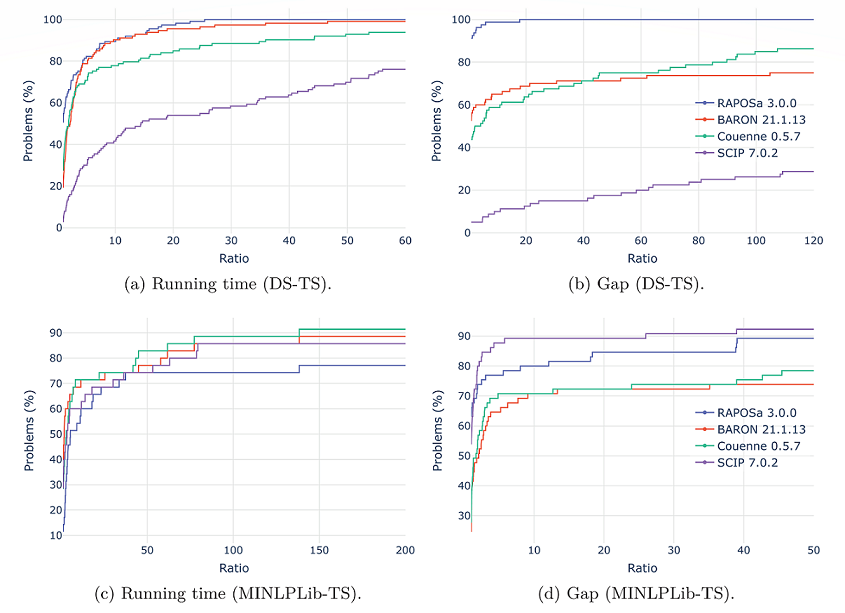
RAPOSa has been benchmarked with general global optimization solvers for nonlinear programming problems like BARON, Couenne and SCIP using two different test sets: DS-TS (taken from [5] and it can be downloaded in AMPL and .nl format at DS-TS) and MINLPLib-TS (taken from www.minlplib.org and it can be downloaded in AMPL and .nl format at MINLPLib-TS).

The four graphics show the performance profiles ([7]). The graphics located on the left represent the performance associated with the running time, while the graphics on the right show those related with the optimality gap.

The figure shows that, in instances from DS-TS, RAPOSa performs better than BARON, Couenne and SCIP. The difference becomes especially notorious in the difficult problems, those that were not solved in less than 10 minutes. On the other hand, in instances from MINLPLib-TS, RAPOSa performs better than BARON and Couenne in terms of optimality gap while it performs worse in terms of time.

More details on these tests can be seen in [8].

How to cite RAPOSa

To cite RAPOSa please refer to this recently accepted paper in the Journal of Global Optimization: https://doi.org/10.1007/s10898-022-01229-w

Core developing team

• Ignacio Gómez Casares (Univ. de Santiago de Compostela)
• Julio González Díaz (Univ. de Santiago de Compostela)
• Brais González Rodríguez (Univ. de Santiago de Compostela)
• Beatriz Pateiro López (Univ. de Santiago de Compostela)

Other collaborators

• Current collaborators: Gabriel Álvarez Castro, Bissan Ghaddar, and Iria Rodríguez Acevedo
• Past collaborators: Raúl Alvite Pazo, Samuel Alvite Pazo, Pepa Arán Paredes, Ángel M. González Rueda, Joaquín Ossorio Castillo, Sofía Rodríguez Ballesteros, Sergio Rodríguez Delgado, Diego Rodríguez Martínez, and David Rodríguez Penas

Bibliography

[1]: Sherali, H. D. and Tuncbilek, C. H., 1992. A global optimization algorithm for polynomial programming problems using a reformulation-linearization technique. Journal of Global Optimization, 2(1), pp. 101-112.

[2]: Sherali, H. D., Dalkiran, E. and Liberti, L., 2012. Reduced RLT representations for nonconvex polynomial programming problems. Journal of Global Optimization, 52(3), pp. 447-469.

[3]: Sherali, H. D., Dalkiran, E. and Desai, J., 2012. Enhancing RLT-based relaxations for polynomial programming problems via a new class of v-semidefinite cuts. Computational Optimization and Applications, 52(2), pp. 483-506.

[4]: Dalkiran, E. and Sherali, H.D., 2013. Theoretical filtering of RLT bound-factor constraints for solving polynomial programming problems to global optimality. Journal of Global Optimization, 57(4), pp. 1147-1172.

[5]: Dalkiran, E. and Sherali, H.H., (2013). RLT-POS: Reformulation-Linearization Technique-based optimization software forsolving polynomial programming problems. Mathematical Programming Computation, 8, pp. 337–375.

[6]: Gay, D. M., 2005. Writing .nl files. Optimization and Uncertainty Estimation.

[7]: Dolan, E. D. and Moré J. J., 2002. Benchmarking optimization software with performance profiles. Mathematical Programming, 91, pp. 201–213.

[8]: González-Rodríguez, B., Ossorio-Castillo J., González-Díaz J., González-Rueda A. M., Rodríguez-Penas D. and Rodríguez-Martínez D., 2022. Computational advances in polynomial optimization: RAPOSa, a freely available global solver. Journal of Global Optimization, In press.